一个特殊子集和问题, 以及指数复杂度下常数优化的意义

一道从朋友那里听到的面试题:

$\sqrt 1, \sqrt 2, \cdots, \sqrt{50}$ 这 50 个数分成两部分, 要求两部分的和最接近. 问这两个和的差最小是多少.

解析分析

(2019-12-07 update: 这个证明数学上是错误的. CLT 在数学上误差项是对于累积分布函数的估计 (Berry-Esseen thm), 收敛速度达不到 $O(2^N)$ 的话就没有办法应用在这个场景里. 一个更直观的论证是, CLT 在 i.i.d 下总是有效, 但把根号和改成 i.i.d. 给出 $O(1)$ 的误差. )

首先从算法角度看, 这个问题非常类似于子集和问题, 除非自然数的平方根有什么特殊的性质可以用到, 这是个 NPC 问题. 用程序严格计算的话, 指数复杂度是跑不掉的. $2^{50}\approx 10^{15}$ 于是我的第一想法是基本上就不要想在自己电脑上解决它了.

简单试了一下优化算法, 可以很轻易的把这个差优化到 $10^{-12}$ 量级, 相比 $\sqrt n$ 几乎可以认为子集和是连续的. 所以我想到的解答是把它连续化.

考虑所有这 50 个数的所有子集和, 一共 $2^{50}$ 个数的分布, 视为随机变量:

\[X = \sum_n X_n \equiv \sum_n \sqrt n l_n\]

其中 $l_n \sim \{0, 1\}$ i.i.d 等概率两点分布. $X$ 的分布, 最直接的猜测是近似正态分布. 检查一下中心极限定理的那么多版本, 注意到 Lyapunov CLT 的要求是:

\[\begin{align*} &s_n^2 = \sum_i^n D[X_i] \\ \exists\,\delta>0 \text{ s.t. } &\lim_{n\to\infty}\frac{1}{s_n^{2+\delta}}\sum_i^n E\big[|X_i - E X_i|^{2+\delta}\big] \end{align*}\]

对于上面给定的 $X_i$,

\[\begin{align*} &DX_n = \frac n4 \\ &s_n^{2+\delta} = \left(\sum_i^n \frac n4 \right)^{1+\delta/2} \sim n^{2+\delta}\\ &\sum_i^n E\big[|X_i - E X_i|^{2+\delta}\big] = \sum_n \frac 14 n^{1+\delta/2} \sim n^{2+\delta/2} \end{align*}\]

Lyapunov CLT 的条件, 对于任意的 $\delta > 0$ 都是成立的. 上面定义的随机变量 $X\sim N(\mu, \sigma^2)$ 有 ($N=50$):

\[\begin{align*} &\sigma^2 = DX = \sum D X_i = \frac 14 \sum_n = \frac 18 N(N+1) (= 318.75) \sim \frac 18 N^2\\ &\mu = EX = \frac 12 \sum_{n=1}^{N} \sqrt n (\approx 119.52 \approx 6.7\sigma) \sim \frac 13 N^{3/2} \end{align*}\]

总共有 $2^{N}$ 个样本, 对于 $X\sim N(\mu, \sigma^2)$ 来说均值以上的第一个样本, 大约出现在:

\[\sigma \Phi^{-1}\left(\frac 12 + 2^{-N}\right) \approx \frac{2^{-N}\sigma}{1/\sqrt{2\pi}} = 2^{-N}\sqrt{\frac \pi 4 N(N+1)} \approx 4\times 10^{-14}\]

CLT 的应用, 对于 50 个数的和, 收敛小于 $\sqrt N$. 另外第一个样本出现是一个概率估计, 所以实际上的结果应该比这个数字大一个 $O(1)$ 的系数. 后文的分析显示确实只有大约 2 倍.

总的来说对于 $\sqrt 1,\sqrt 2,\cdots, \sqrt N$ 的子集和, 最小差随 $N$ 的渐近关系是 $\sim N2^{-N}\sqrt{\pi/4}$.

程序计算

后来从朋友处听到的更新是, 有办法改进复杂度的常数, 使得指数上只有 $N/2$, 而 $2^{25}\approx 3\times 10^7$ 在现代计算机上就是可行的 (考虑 CPU 可以做到 $10^{10}$ FLOPS).

算法的思路是:

1. 取其中 25 个数, 计算所有的子集和 $s_i$ 并排序, $O(n\log n)$
2. 取余下的 25 个数, 计算子集和 $s’_i$ 并在上一步得到的序列中二分查找 $s_j$ 使得 $s’_i + s_j$ 最接近全体和的一半, $O(n\log n)$
3. 记录上述结果的最小值

需要注意的是, 前面的分析发现这个差只有 $10^{-14}$, 相对误差 $10^{-16}$, 和双精度浮点截断误差 $2^{-52}$ 是同一个量级了. 所以或者使用更高的浮点数精度, 或者要小心翼翼得处理浮点数问题.

一个加入了 OpenMP 并行, 使用快排的 C 程序见这里. 运行的结果是, 大于 50 个数和的最小数, 是这些数的和: 2, 3, 4, 5, 6, 10, 11, 14, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 28, 29, 32, 34, 35, 39, 40, 42, 50.

当然这个解不唯一, 比如将 16 换成 1 和 9 的结果时候一样的. 这些数的平方根和, 比起 50 个数的和的一半大了 $7.15\times 10^{-14}$. 得到正确的差, 前提是使用 long double 类型计算, 以及使用匹配的 sqrtl 计算平方根.

写这段程序的过程, 学到了三件小事:

1. 不要看到指数复杂度就止步不前. 指数意味着对不太大的问题规模, 计算量就会很大, 但也意味着常数项的优化是显著的.
2. OS 对于栈内存的使用是有限制的. 在这个程序中如果 $2^{25}$ 个数作为静态内存写入程序的话, 会导致段错误 (x64 Linux/gcc)
3. 练习了快排以及求取最大值的并行化

---

2020-01-07 更新 闲来无事画了个图, 把 1,2,…,25 的平方根求和做了个图, 如下

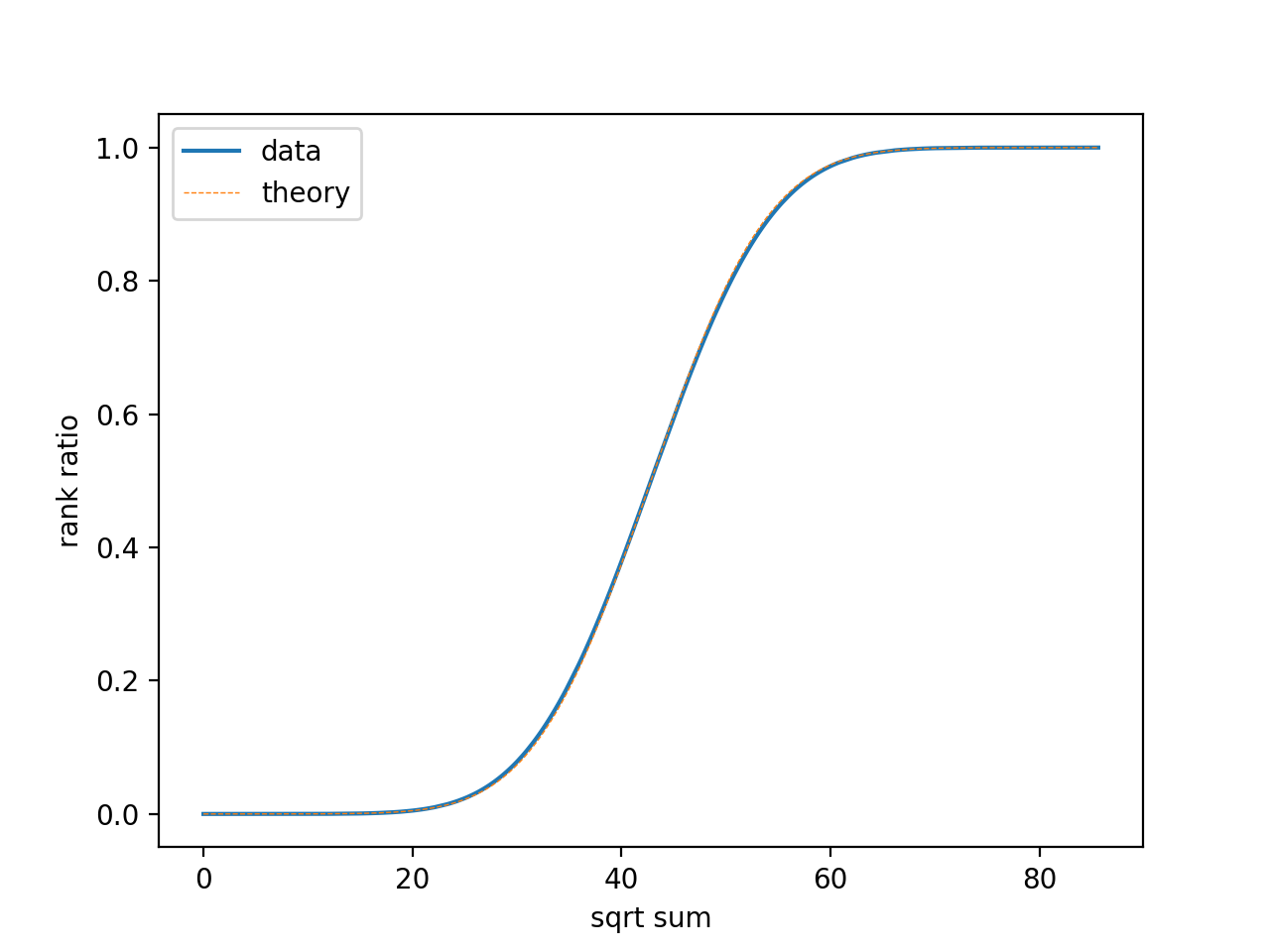
其中横轴是求和值, 纵轴是归一化到 0~1 的排序位置, 虚线是按照前面有误的解析分析给出的正态分布

\[X\sim N\left(\frac 12 \sum_{n = 1}^{N} \sqrt{n}, \frac 18 N(N+1) \right) \qquad (N=25)\]

发现拟合得极好. 进一步计算这些和的均值和方差与理论值差别在 $10^{-13}$ 量级. 其中均值由于对称性不应有估算误差, 所以这应该来自浮点误差积累. 理论值和实验值的差别作图如下:

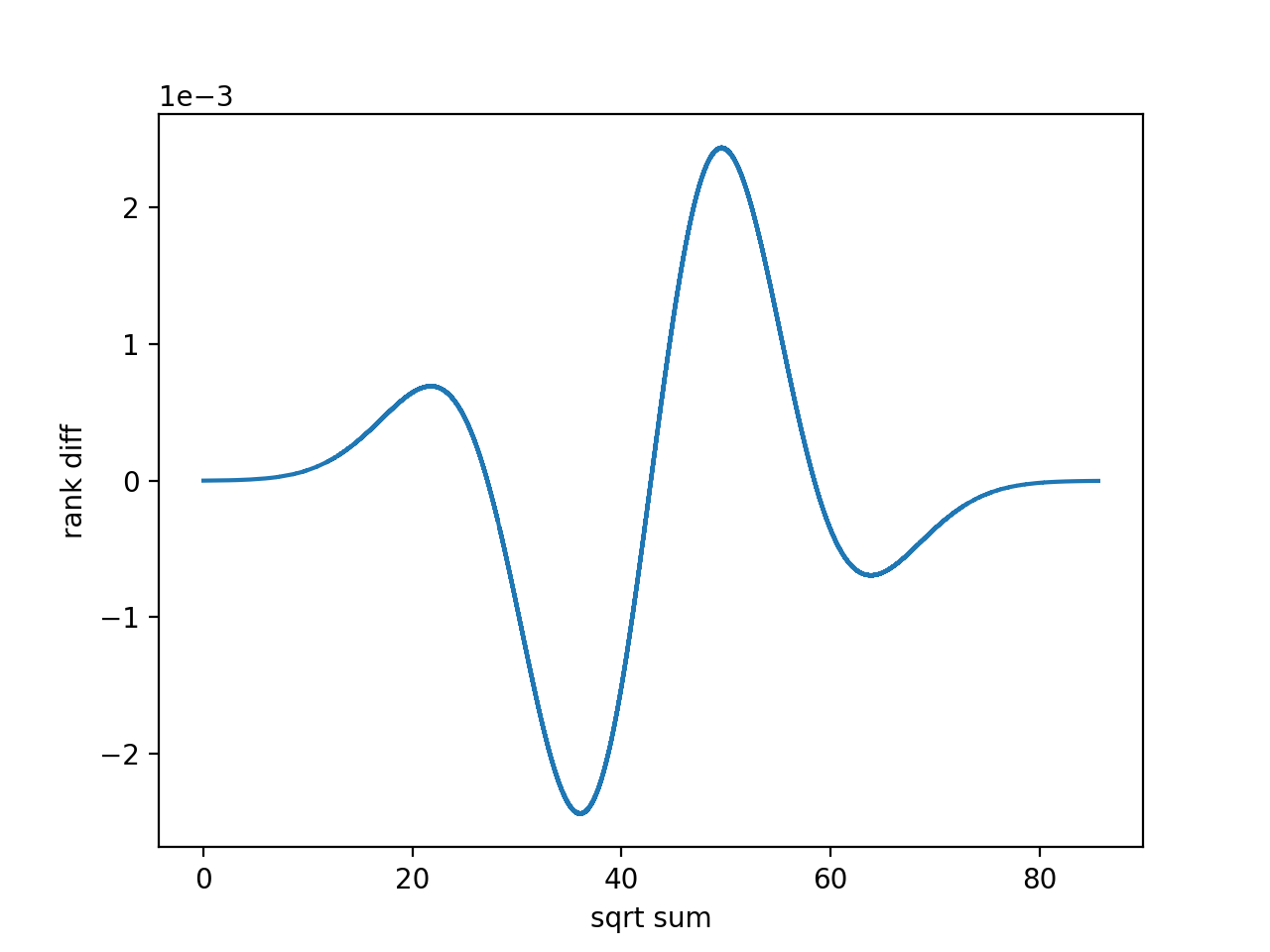
所以这个正态分布的猜测仍然应该是正确的, 并且误差应该也可以估算. 可惜上面的这个证明不对.