Majorana 零能模
这是上学期课程的一次文章阅读报告, 想着据此写一篇博客结果拖延症到现在了. 报告的演示文稿这里. 文章Nadj-Perge, Stevan et al. (2014). “Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor”. In: Science 346.6209, pp. 602–607.
Majorana (马拉约那) 费米子
马拉约那费米子是服从费米统计, 并且反粒子是自身的费米子. 在凝聚态体系中的数学表达式即为产生算符等于湮灭算符 $\gamma_i = \gamma_i^\dagger $ (凝聚态含义下的反粒子即空穴, 其产生算符即正粒子的湮灭算符), 当然它是费米子, 还要加入反对易关系 $ \{\gamma_i, \gamma_j\} = 2\delta_{ij}$. 这样的费米子表现出一些有趣的性质, 包括
- 粒子数算符 $\gamma^\dagger\gamma $ 没有意义, 因为是常数;
- 不带电/不具有守恒荷;
- 没有质量 (能量);
- ……
真空中是否真的存在马拉约那费米子尚没有定论. 有的理论认为中微子是马拉约那费米子, 有的理论认为暗物质和马拉约那费米子有关.
概念上, 马拉约那算符可以从费米子中构造: $ c_i = \frac 12 (\gamma_{i1} + \mathrm i \gamma_{i2}) $ 这样的构造方法实际上引入了新的自由度, 或者换言之这里的马拉约那算符实际只拥有 “半个” 自由度. 而这种模式的激发可以在凝聚态体系中找到. 由于前面已经讨论马拉约那粒子不存在有意义的粒子数算符, 所以这种激发一定是零能的. 称半个自由度总是很奇怪, 所以我更喜欢把这种激发称为马拉约那零能模的提法.
Kiteav 模型
这是一个 (可能是) 最简单的能表现出马拉约那零能模的模型. 模型的结论大致是说一维的超导体在两端具有一个零能量的态, 具有 Majorana 费米子的一些特征. 一维超导体的紧束缚模型哈密顿量如:
\[H = -\mu\sum_{i=1}^N c_i^\dagger c_i - \sum_{i=1}^{N-1} (t c_i^\dagger c_{i+1} + \Delta c_i c_{i+1} + \mathrm{H.c})\]其中 $\Delta$ 项是相互作用项的平均场近似. 特别的, 对于 $\mu=0$, $t=\Delta$ 的情形, 这个哈密顿量可以简单对角化为
\[H = -\mathrm i t \sum_{i=1}^{N-1}\gamma_{i,2}\gamma_{i+1,1} = 2t\sum_{i=1}^{N-1}\tilde c_i\tilde c_i\]其中狄拉克费米子准粒子的激发 $\tilde c_i=(\gamma_{i+1, 1}+\mathrm i\gamma_{i, 2})/2$.
注意到对角化的激发模式比自由度少一项, 说明还有一个零能的模式, 表达为: $c_M = (\gamma_{N,2} + \mathrm i \gamma_{1,1})/2$. 如图:
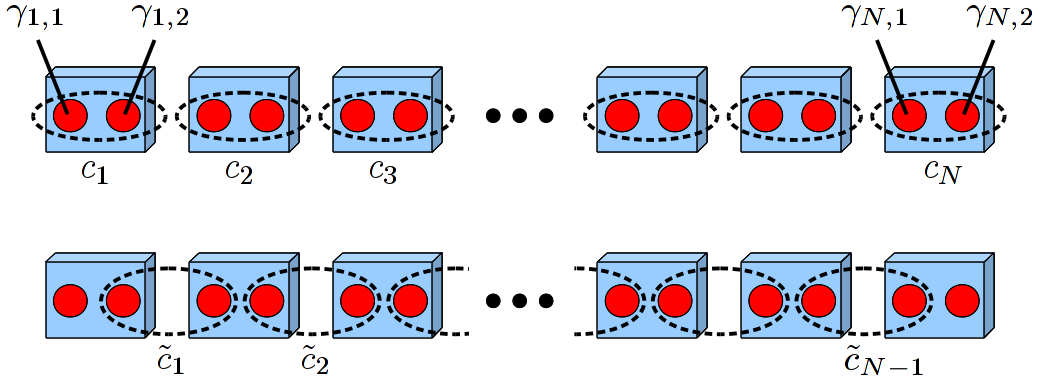
对于一般的参数, 只要 $|\mu|<2t$, 并且一维链足够长, 这一模式仍然存在, 只不过不完全局限在两端, 而是一个沿着一维链指数衰减的模式. 这个零能模如果只看一端的话, 表现就应当和马拉约那费米子相当. 与此同时,这一模型的基态, 满足大家所感兴趣的拓扑序的性质:
- 简并的基态, 以及与激发态之间有能隙
- 简并来源于对称性, 而非参数敏感: $\mathbb Z_2 $ 的粒子-空穴对称
- 这一模式是非局域的
理想的情况下, 如果能在二维环境里实现类似的模型, 这种激发模式可以产生任意子 (Anyon) 并用于拓扑量子计算.
[1]Leijnse, Martin and Karsten Flensberg (2012). “Introduction to topological superconductivity and Majorana fermions”. In: Semiconductor Science and Technology 27.12, p. 124003.
[2]Kitaev, A Yu (2001). “Unpaired Majorana fermions in quantum wires”. In: Physics-Uspekhi 44.10S, p. 131.
自旋简并与自旋轨道耦合
要构造一个能实现 Kitaev 模型的环境, 首先要构造一维超导, 但这还不够. 一个很严重的问题是 Kiteav 是无自旋的. 自旋会产生简并从而破坏我们需要的性质:
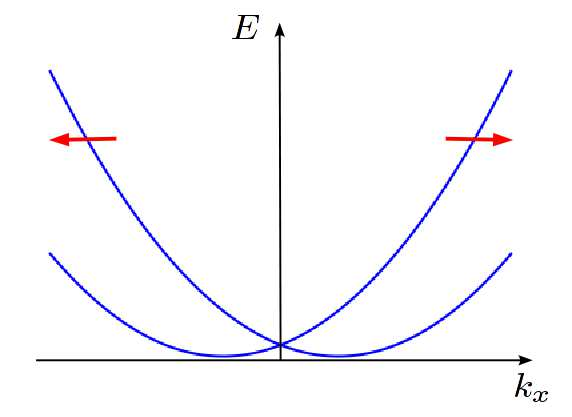
要找到一个能带结构和无自旋体系相似的环境,我们需要引入自旋-轨道耦合打开上图中的能带简并.
实验平台
该实验使用的是超导铅表面生长的一维铁原子链. 确认实验平台具有如下特征:
- 铁磁性 (通过极化的 STM/STS 针头测量电导率, 观察磁滞现象)
- 基质的自旋轨道耦合 (极化 STM 在基质上电导对电流的不对称)
- 超导体的带隙
主要的实验手段是在不同条件下用 STS 扫描 LDOS (局部态密度, Local Density of State, 态密度乘对应的态的空间分布, 即波函数模方), 先依次验证上述各性质, 而后检验零能模:
- 在铁原子链的两端, LDOS 具有零能量的峰值 (ZBP, Zero Bias Peak), 说明存在分布于一维链两端的零能模, 于马拉约那零能模的预测相符
实验结果在博文开头提到的文献中, 不再引用.

留下评论