平衡二叉树 (AVL树, 红黑树) 以及 Python 上的一组最小实现
Intro
Python 自带的数据结构中并没有平衡二叉树, 在刷 Leetcode 某题的时候看到需求. 网上一查现成的轮子都巨大无比… 于是自己做了个实现, 顺便复习复习邓公的课.
平衡二叉树保证即便在最坏情况下, 插入, 删除和检索数据都保持在 $O(\log n)$ 复杂度, 插入和删除完成后的调整复杂度也是 $O(\log n)$ . 红黑树比起 AVL 树, 在最坏情况下结果是一样的, 但优势在于, 调整的平均复杂度是 $O(1)$ . 知乎上有 网友测试 的结果是, AVL 树如果加上及时的退出机制时, 性能并没有显著差于红黑树.
所谓最小实现, 即:
- 结点不记录父结点 (话说, 父结点这个词有没有政治正确问题啊?), 而是在每次寻找结点时记录祖先节点
- 对于 AVL 树来说, 每个结点仅额外包含高度信息
- 对于红黑树来说, 每个结点用一个布尔变量记录颜色
- 为了速度避免递归而使用栈模拟递归, 于是也能在确定已经恢复平衡时提前退出循环
- 为了减少一半内存占用而避免虚拟的空叶结点
- 树对外的接口表现为一个检索器, 添加, 删除和搜索都按值进行. 删除不存在的值时直接报错
这组实现中, 还有几处希望能改进的地方, 但暂时不知道要如何平衡代码的优雅和性能暂且搁置了:
- 两个树没能实现共用代码的基类
- 记录祖先节点的栈同时需要记录左孩子/右孩子信息, 有信息冗余的嫌疑
- 红黑树的旋转和重上色往往同时发生, 应当可以多一层抽象来减少重复代码
- 最小实现中没能提供按位置插入和删除的接口, 从而没法复用搜索过程的运算
AVL 树
AVL 树的重平衡只需要一到两次左旋或者右旋操作即可.
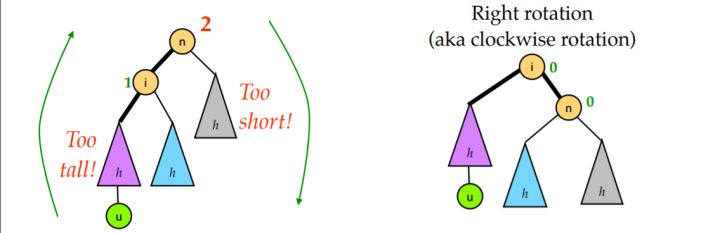
其中右旋操作如下图, 结点经过右旋变为其原左孩子的右孩子. 左旋操作是它的镜像对称.
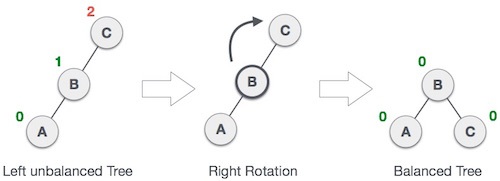
需要平衡时, 分成如下四中情况:
- LL 型: 左孩子的左孩子太高, 进行一次右旋即可
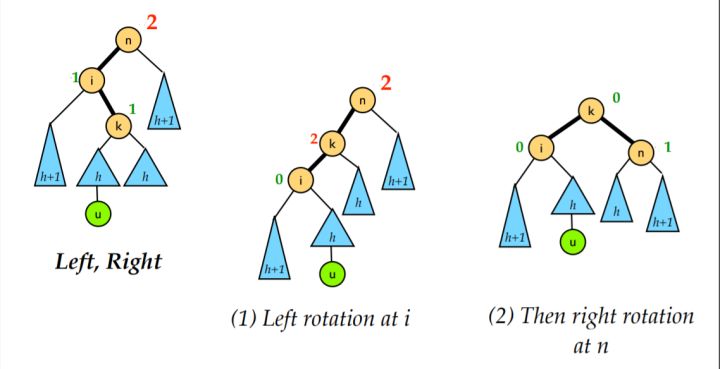
- LR 型: 左孩子的右孩子太高, 对左孩子进行一次左旋之后之后变成 LL 型
- RR 型: LL 型的镜像对称
- RL 型: LR 型的镜像对称
据此, AVL 树的结点需要的实现如下:
class AVLTreeNode():
def __init__(self, val):
self.left = None
self.right = None
self.val = val
self.height = 1
def updateHeight(self):
self.height = 1 + max(
self.left.height if self.left else 0,
self.right.height if self.right else 0)
def rotateRight(self):
newSelf = self.left
self.left = newSelf.right
newSelf.right = self
self.updateHeight()
newSelf.height = max(newSelf.height, self.height + 1)
return newSelf
def rotateLeft(self):
newSelf = self.right
self.right = newSelf.left
newSelf.left = self
self.updateHeight()
newSelf.height = max(newSelf.height, self.height + 1)
return newSelf
def bFactor(self):
return ((self.left.height if self.left else 0) -
(self.right.height if self.right else 0))
def reBalance(self):
bf = self.bFactor()
if bf > 1:
if self.left.bFactor() < 0:
# LR case
self.left = self.left.rotateLeft()
# LL and LR case
return self.rotateRight()
if bf < -1:
if self.right.bFactor() > 0:
# RL case
self.right = self.right.rotateRight()
# RR and RL case
return self.rotateLeft()
# balanced
return self
其中由于不记录父结点=, 每次旋转或者重新平衡操作后, 需要返回变换后处在当前位置的结点, 由调用者更新树的连接.
检索时, 返回检索值在树的数据中的上下相邻元素, 特别的, 当检索值存在时, 两个返回值都等于检索值. 插入和删除时, 先检索到合适的位置, 同时用栈记录从根结点到相关结点路径 (祖先节点), 而后回溯调整. 特别的, 当
- 插入后, 遇到任何一个不再需要调整高度的祖先结点, 可以提前结束回溯
- 删除时, 若要删除的结点不是叶结点, 则需要先和后继 (右子树的最小结点) 交换后再删除后继结点
- 删除后, 当发现某个结点的高度不需要更新, 且不需要旋转时, 可以提前结束回溯
class AVLTree(): def __init__(self): self.root = None def search(self, val): n1 = None n2 = None c = self.root while c: if c.val == val: return val, val if val < c.val: n2 = c.val c = c.left else: n1 = c.val c = c.right return n1, n2 def insert(self, val): c = self.root stack = [] while c: if val < c.val: stack.append((c, True)) c = c.left else: stack.append((c, False)) c = c.right c = AVLTreeNode(val) while stack: prt, isleft = stack.pop() if isleft: prt.left = c else: prt.right = c if c.height < prt.height: # height of prt not changed return prt.height = max(c.height + 1, prt.height) c = prt.reBalance() self.root = c def delete(self, val): """Raise if val doesn't exist""" c = self.root stack = [] while c.val != val: if val < c.val: stack.append((c, True)) c = c.left else: stack.append((c, False)) c = c.right # delete c if c.right: # replace c by min of c.right c.right, c.val = self.deleteMin(c.right) c.updateHeight() else: # replace c by c.left c = c.left while stack: prt, isleft = stack.pop() if isleft: prt.left = c else: prt.right = c oldh = prt.height prt.updateHeight() c = prt.reBalance() if oldh == prt.height and c == prt: return self.root = c def deleteMin(self, node): c = node stack = [] while c.left: stack.append(c) c = c.left minVal = c.val c = c.right while stack: prt = stack.pop() prt.left = c oldh = prt.height prt.updateHeight() c = prt.reBalance() if oldh == prt.height and c == prt: c = node break return c, minVal
红黑树
红黑树满足:
- 每个结点是红色或者黑色
- 根结点是黑的
- (虚拟的) 每个叶结点都是黑的
- 对于不使用虚拟结点作为叶结点的实现, 则左右孩子均空的叶结点是红色的
- 如果一个结点是红的, 那么它的两个孩子都是黑的
- 对于不使用虚拟结点作为叶结点的实现, 则孩子是黑或空
- 对于任意结点而言, 其到叶结点树的每条路径都包含相同数目的黑结点
- 下称这个数目为黑色高度, 特别的, 空树的黑色高度为 1
红黑树的结点中可实现的方法有限, 大多数更新操作都要依赖祖父结点和叔叔结点, 所以只能在外部完成:
class RBTreeNode():
def __init__(self, val=None):
self.left = None
self.right = None
self.val = val
self.red = False
def rotateRight(self):
newSelf = self.left
self.left = newSelf.right
newSelf.right = self
return newSelf
def rotateLeft(self):
newSelf = self.right
self.right = newSelf.left
newSelf.left = self
return newSelf
def lred(self):
return self.left and self.left.red
def rred(self):
return self.right and self.right.red
红黑树插入结点时, 插入的结点默认是红色, 于是需要解决双红色问题:
- 父结点黑色, 问题解决
- 当前结点是根结点, 涂黑即可
- 父结点是红色, 则祖父结点黑色
- 叔叔结点是红色: 父结点和叔叔结点涂黑, 祖父结点涂红, 当前结点变为祖父结点,
变成余下两种情况之一
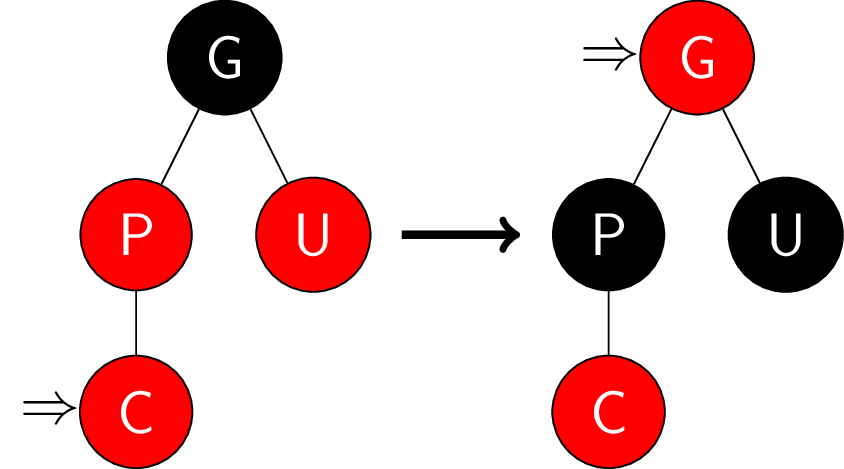
- 叔叔结点黑色且当前结点和父结点不同侧:
例如当前结点是右孩子, 父结点是左孩子, 则父结点左旋,
从而当前结点和父结点交换关系, 祖父结点不变, 变成余下的情况
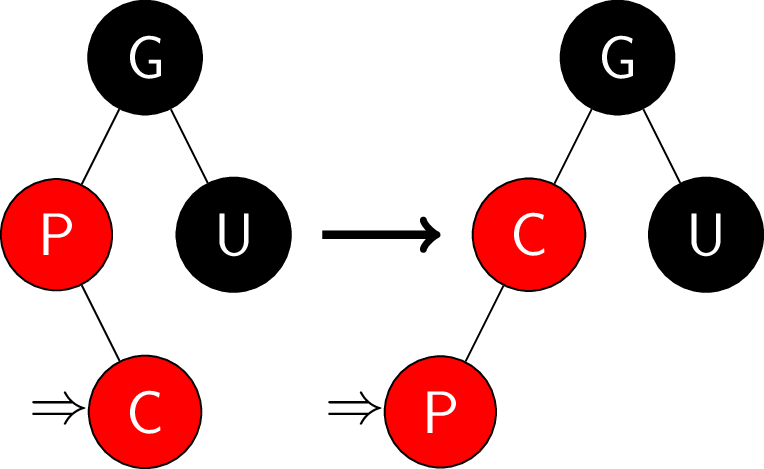
- 叔叔结点黑色且当前结点和父结点同侧: 父结点涂黑, 祖父结点旋向另一侧且涂红
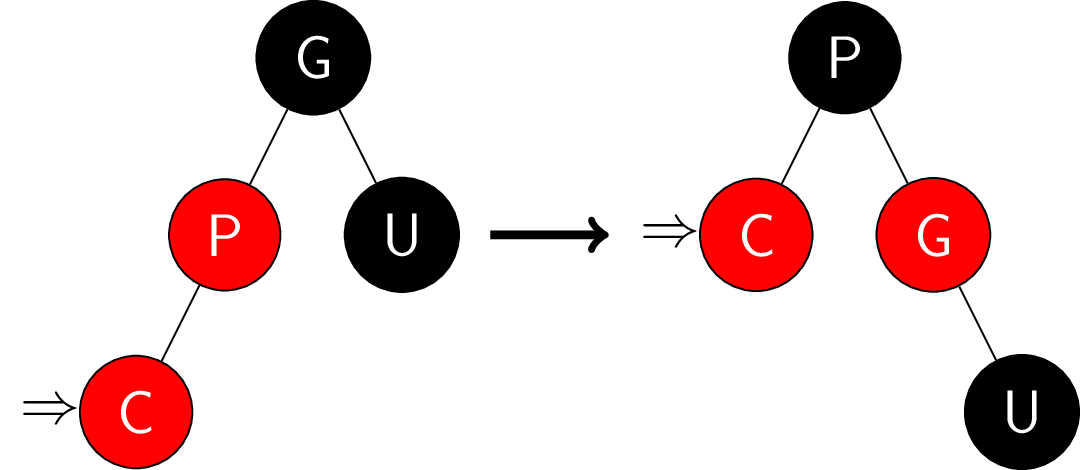
- 叔叔结点是红色: 父结点和叔叔结点涂黑, 祖父结点涂红, 当前结点变为祖父结点,
变成余下两种情况之一
以上操作均不改变子树的黑色高度, 从而能保持子树的红黑树性质; 操作 1, 3 实际上使得当前结点向上移, 于是能逐渐传递到根结点.
class RBTree():
def __init__(self):
self.root = None
def search(self, val):
n1 = None
n2 = None
c = self.root
while c is not None:
if c.val == val:
return val, val
if val < c.val:
n2 = c.val
c = c.left
else:
n1 = c.val
c = c.right
return n1, n2
def attach(self, stack, node):
if stack:
if stack[-1][1]:
stack[-1][0].left = node
else:
stack[-1][0].right = node
else:
self.root = node
def insert(self, val):
if self.root is None:
self.root = RBTreeNode(val)
return
c = self.root
stack = []
while c:
if val < c.val:
stack.append((c, True))
c = c.left
else:
stack.append((c, False))
c = c.right
c = RBTreeNode(val)
self.attach(stack, c)
c.red = True
prt, isleft = stack.pop() # parent
while prt and prt.red:
gp, gisleft = stack.pop() #grand-parent
if gisleft:
uncle = gp.right
if uncle and uncle.red:
prt.red = False
uncle.red = False
c = gp
c.red = True
prt, isleft = stack.pop() if stack else (None, False)
else:
if not isleft:
c = prt
prt = c.rotateLeft()
gp.left = prt
# so c is prt.left
prt.red = False
gp.red = True
prt = gp.rotateRight()
self.attach(stack, prt)
else:
uncle = gp.left
if uncle and uncle.red:
prt.red = False
uncle.red = False
c = gp
c.red = True
prt, isleft = stack.pop() if stack else (None, False)
else:
if isleft:
c = prt
prt = c.rotateRight()
gp.right = prt
prt.red = False
gp.red = True
prt = gp.rotateLeft()
self.attach(stack, prt)
self.root.red = False
删除结点时, 首先和 AVL 相同的策略找到可以删除的叶结点. 若删除的结点是红色, 则红黑树的性质保持, 可以直接结束. 否则视为替换在此处的结点多了一层黑色, 向上传递多余的黑色以恢复红黑树性质:
- 当前结点本来是红色: 涂黑即可, 红黑树性质恢复
- 当前结点是根结点: 多余的黑色可以扔掉, 红黑树性质恢复
- 当前结点本来是黑色: 双重黑色, 据此父结点的另一个子树 (以兄弟结点为根) 的黑色高度至少为 2,
兄弟结点非空
- 兄弟结点红色: 从而父结点黑色.
将父结点涂红, 兄弟结点涂黑, 并将父结点旋至当前结点同侧, 原兄弟结点变祖父结点,
兄弟结点变成原兄弟结点的子结点, 是黑色的, 从而变成余下的三种情况
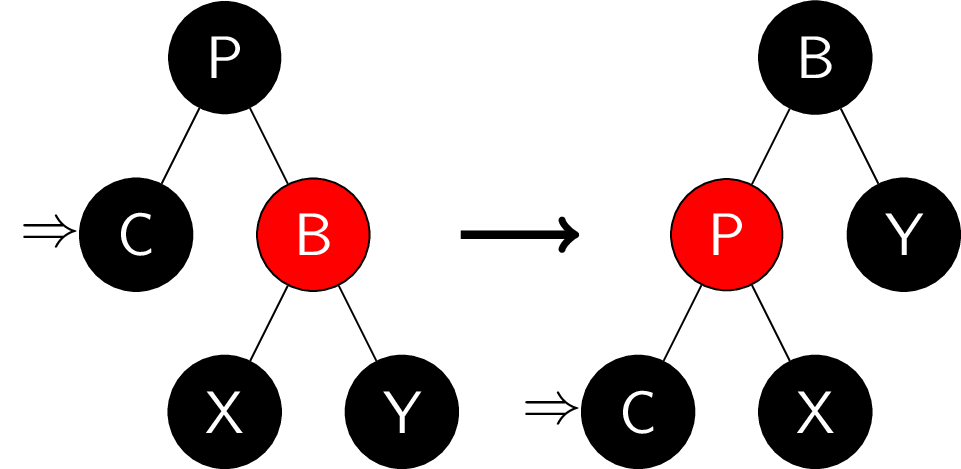
- 当前结点和兄弟结点均为黑色, 且兄弟结点的子结点均为黑色 (即兄弟结点可以是红色):
将兄弟结点涂红, 当前结点变为父结点 (带上多一层黑, 若原来是红色则变为前述恢复的情况)
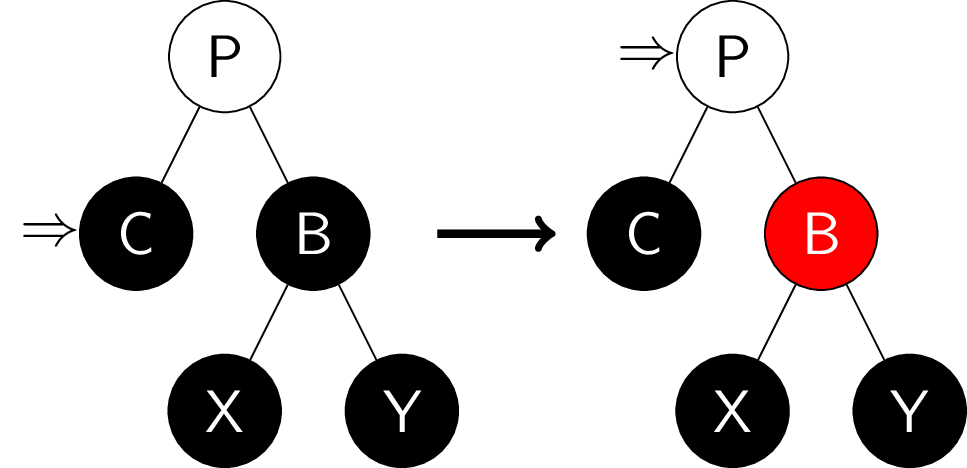
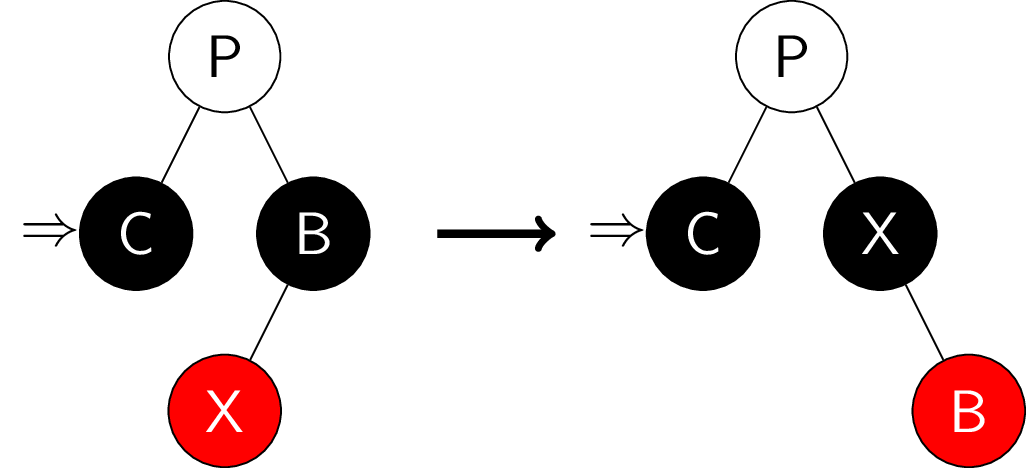
- 当前结点和兄弟结点均为黑色, 且兄弟结点与当前结点异侧的子结点是黑色, 同侧子结点是红色:
将兄弟结点的同侧子结点涂黑, 兄弟结点涂红且旋向另一侧, 从而变成余下的情况
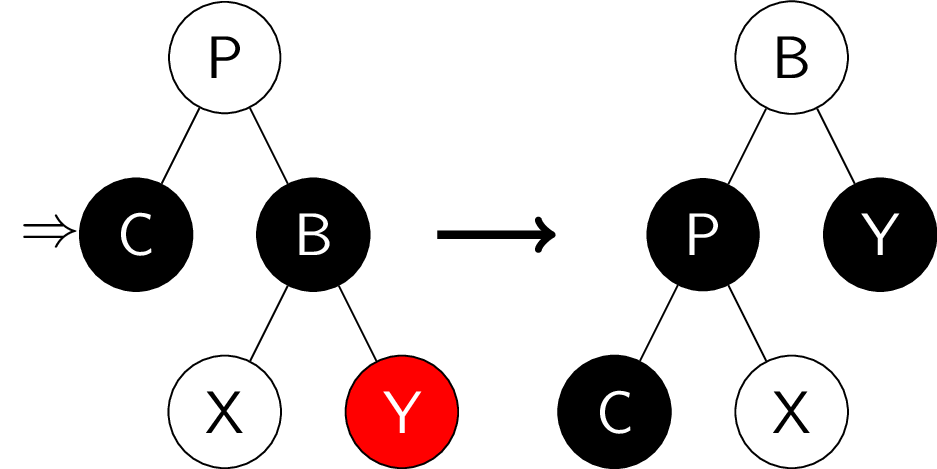
- 当前结点和兄弟结点均为黑色, 且兄弟结点与当前结点异侧的子结点是红色, 同侧子结点颜色任意:
兄弟结点改为父结点颜色, 父结点和兄弟结点的异侧子结点涂黑,
父结点旋向当前结点一侧. 这个操作将原兄弟结点变为父结点, 其当前结点一侧的子树,
以原父结点为根, 黑色高度 +1, 从而解决了双重黑色的问题, 红黑树性质恢复
- 兄弟结点红色: 从而父结点黑色.
将父结点涂红, 兄弟结点涂黑, 并将父结点旋至当前结点同侧, 原兄弟结点变祖父结点,
兄弟结点变成原兄弟结点的子结点, 是黑色的, 从而变成余下的三种情况
(上述 “当前结点” 可以是虚拟的空叶结点)
def delete(self, val):
c = self.root
stack = []
while c.val != val:
if val < c.val:
stack.append((c, True))
c = c.left
else:
stack.append((c, False))
c = c.right
if c.left is None:
x = c.right
elif c.right is None:
x = c.left
else:
# replace c by min of c.right
stack.append((c, False))
minRight = c.right
while minRight.left:
stack.append((minRight, True))
minRight = minRight.left
c.val = minRight.val
c = minRight
x = c.right
# delete c
self.attach(stack, x)
if c.red:
return
# fix color
while stack and not (x and x.red):
prt, isleft = stack.pop()
if isleft:
bro = prt.right
if bro.red:
bro.red = False
prt.red = True
self.attach(stack, prt.rotateLeft())
# prt.rotate return bro
stack.append((bro, True))
bro = prt.right
# now bro is black
if not bro.lred() and not bro.rred():
bro.red = True
x = prt
else:
if not bro.rred():
# so bro.lred() == True
bro.left.red = False
bro.red = True
bro = bro.rotateRight()
prt.right = bro
# so bro.rred() == True
bro.red = prt.red
prt.red = False
bro.right.red = False
self.attach(stack, prt.rotateLeft())
# prt.rotate return bro
stack.append((bro, True))
x = self.root
break
else:
bro = prt.left
if bro.red:
bro.red = False
prt.red = True
self.attach(stack, prt.rotateRight())
stack.append((bro, False))
bro = prt.left
if not bro.lred() and not bro.rred():
bro.red = True
x = prt
else:
if not bro.lred():
bro.right.red = False
bro.red = True
bro = bro.rotateLeft()
prt.left = bro
bro.red = prt.red
prt.red = False
bro.left.red = False
self.attach(stack, prt.rotateRight())
stack.append((bro, False))
x = self.root
break
x.red = False
后记
要不是刷 Leetcode 心血来潮实现一下 Python 的二叉树, 都没发现自己代码能力下降得这么厉害.. 当年选邓公的课的时候, 还能半天手撸 C++ 红黑树, debug 完成 OJ 题目, 如今用 Python 实现一下 AVL 树都要一天…
然后实验就又拖下了…

留下评论