跳转表 (skiplist) 的期望分析

Intro

写这篇博文的主要原因是发现, 中文互联网上竟然没有看到过关于跳转表时间性能的定量分析… 英文也只有学术文献而没有简单的版本.

写完二叉树, 看看另一种更容易实现的 $O(\log N)$ 检索/插入/删除的数据结构: skiplist. 当然容易实现的是指随机跳转表. 通常来说它的表现是要差于二叉树的, 但因为检索和恢复的过程只影响局域的链表链接, 尤其适用于高并发的场景.

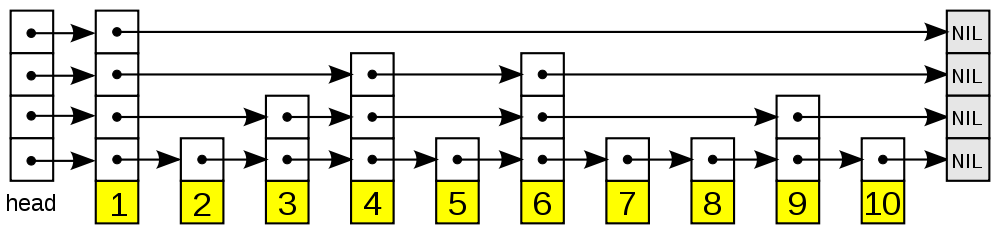
简单说就是每一层是个链表, 而后每个结点以概率 $p$ 保留到下一层. 最底层是全部数据. 从顶部开始做检索, 自顶而下进行. 常见的取法是 $p=1/2$.

以下内容记 $h_n$ 为第 $n$ 个结点的高度, $h = \max{h_n}$ 为总的高度, $l_i = \sum_n \mathbb I \big[h_n \ge i\big]$ 为第 $i$ 层的结点数量, 数据总量 $N$.

一组最简单的 Python 实现附于文末.

空间性能

空间性能是相对容易计算的. 每一层的结点数量期望都是上一层期望的 $p$:

\[E[l_i] = E_{l_{i-1}}\big[E[l_i|l_{i-1}]\big] = E_{l_{i-1}}[pl_{i-1}] = pE[l_{i-1}]\]

最低层是全部数据的链表, 即 $l_0 = N = E[l_0]$. 于是总的空间占用期望是

\[E\left[\sum_{i=0}^\infty l_i\right] = \sum_i E[l_i] = E[l_0]\sum_i p^i = \frac{N}{1-p} \sim O(N)\]

若考虑链表实现的额外开销 (如链表头的哨兵), 则和总高度 $h$ 的期望有关, 空间开销为 $O(N+h)$, 其中 $h\sim\log(N)$ 证明如下:

首先计算关于 $h$ 的概率分布:

\[P(h > h') = 1 - \prod_i P(h_i \le h') = 1 - (1-p^{h'})^N\]

于是 $h$ 的期望

\[\begin{align*} E[h] &= \sum_{h'=0}^\infty h' P(h = h') \\ &= \sum_{h'} h'\big(P(h > h') - P(h > h'-1)\big) \\ &= \sum_{h'} P(h>h') = \sum_{h'} \left[1-(1-p^{h'})^N\right] \\ &= \sum_{n=0}^{N-1} \sum_{h'} (1-p^{h'})^n p^{h'} \\ &\sim \sum_n \int_0^1 y^n \frac{\mathrm d y}{-\ln p} \qquad (y = 1-p^{h'}) \\ &= \frac{1}{-\ln p}\left(1 + \sum_{n=1}^{N-1} \frac 1n\right) \\ &\sim \frac{\ln N}{-\ln p} = \log_{1/p}{N} \end{align*}\]

(这个结果一点都不意外: 从 1 开始以 $p$ 的增长率增长到 $N$ 的结果就是这个. 不过一个比较严格的计算过程略微有点费劲, 容易出现把求和拆成两个发散和的错误)

时间性能

在第 $i$ 层结点上搜索的时间, 最大为上一层相邻结点之间的结点数量, 其期望值为 $(l_i - l_{i+1})/(l_{i+1}+1)$, 即:

\[E[t_{i}|l_i, l_{i+1}] = \frac{l_i - l_{i+1}}{l_{i+1} + 1}\]

考虑给定 $l_{i}$, $l_{i+1}\sim B(l_i, p)$ 是二项分布,

\[\begin{align*} E[t_{i}|l_{i}] &= \sum_{l_{i+1}=0}^{l_i} \frac{l_i - l_{i+1}}{l_{i+1} + 1} {l_{i+1} \choose l_i} p^{l_{i+1}} q^{l_i-l_{i+1}} \qquad (q = 1-p)\\ &= \sum_{l_{i+1}} \left(\frac{l_i + 1}{l_{i+1} + 1} - 1\right) {l_{i+1} \choose l_i} p^{l_{i+1}} q^{l_i-l_{i+1}} \\ &= (l_i + 1)\left(\sum \frac{1}{l_{i+1}+1}{l_{i+1}\choose l_i} p^{l_{i+1}}q^{l_i - l_{i+1}}\right) - 1 \\ &= (l_i + 1)\frac{(p+q)^{l_i+1} - q^{l_i+1}}{(l_i+1)p} - 1 \\ &= \frac{1 - (1-p)^{l_i+1}}{p} - 1 \end{align*}\]

所以每一层的期望为

\[\begin{align*} E[t_i] &= \sum_{l_i=0}^N \left(\frac{1 - (1-p)^{l_i+1}}{p} - 1\right) {l\choose n} p^{il} (1-p^i)^{N-l} \\ &= \left(\frac 1p - 1\right) - \frac{1-p}{p} \sum_{l_i} (1-p)^{l_i} {l\choose n} p^{il} (1-p^i)^{N-l} \\ &= \frac 1p - 1 - \frac{1-p}{p} \big[(1-p)p^i + 1-p^i\big]^N \\ &= \frac{1-p}{p} \big[1 - (1-p^{i+1})^N\big] \end{align*}\]

假定向下跳转的消耗和向右跳转的比值为 $\xi$, 搜索所需的时间期望值为

\[\begin{align*} E\left[\sum_{i=0} t_i + \xi\right] &= \xi E[h] + \sum_i E[t_i] \\ &= \xi E[h] + \left(\frac 1p - 1 \right) \sum_i \big[1 - (1-p^{i+1})^N\big] \\ &= \left(\frac 1p - 1 + \xi \right)E[h] \sim \left(\frac 1p - 1 + \xi \right)\log_{1/p}{N} \end{align*}\]

最后一步代入了 $E[h]$ 的计算过程第三行. 这个结果也和挥挥手的结果是一致的: 期望来看, $l_{i+1} = p l_i$, 于是 $t_i = 1/p-1$, 总耗时 $(1/p-1+\xi)h$. (这个一致性可能是个巧合? 不然算了老半天岂不是白费力气… )

其中有结论:

1. 总的时间复杂度 $\mathcal O(\log N)$
2. 最佳的概率 $p^*$ 取决于 $\xi$ : $p^*(\ln 1/p^* - 1) = \xi - 1$
   • 特别的当 $\xi = 1$ 时, $p^* = 1/e$ 是最优解;
   • 当 $\xi\to 0$ 时搜索耗时关于 $p$ 单调递减.

Python 实现

实现了按值插入和删除的接口, 和上一篇平衡二叉树的接口一致. 为了避免存储左边和上边的前序结点, 内部实现的搜索接口需要记录路径.

from random import randrange as rand, random as drand
class QuadList:
    def __init__(self, val=None, right=None, below=None):
        self.val = val
        self.right = right
        self.below = below

class SkipList:
    def __init__(self):
        self.header = QuadList()

    def _search(self, val):
        prevs = []
        c = self.header
        while c.below:
            while c.right and c.right.val < val:
                c = c.right
            prevs.append(c)
            c = c.below
        while c.right and c.right.val < val:
            c = c.right
        return c, prevs

    def _insert(self, val, c, prevs):
        c.right = QuadList(val, c.right)
        c = c.right
        # while rand(2):
        while drand() > 0.632:
            # 0.632 = 1-1/e
            if prevs:
                last = prevs.pop()
            else:
                self.header = QuadList(below=self.header)
                last = self.header
            last.right = QuadList(val, last.right, c)

    def _delete(self, val, c, prevs):
        assert c.right.val == val
        while c.right and c.right.val == val:
            c.right = c.right.right
            if prevs: 
                c = prevs.pop()
            else:
                break
        # clean empty layers
        while self.header.right is None and self.header.below:
            self.header = self.header.below

    def search(self, val):
        c, _ = self._search(val)
        return c.val, c.right.val if c.right else None

    def insert(self, val):
        self._insert(val, *self._search(val))

    def delete(self, val):
        self._delete(val, *self._search(val))

鸣谢

感谢 J.Y. Zhang 和妍姐的讨论! 我发现我做概率题的能力真的是下降的厉害… 做实验降智商…